Actualidad
Este año 2023 es noticia Claudio Ptolomeo (85 – 165), quién fue un astrónomo, astrólogo, químico, geógrafo y matemático griego. El titular:
Hallan la descripción más antigua del meteoroscopio en un tratado perdido de Ptolomeo
Pero Ptolomeo es más conocido por su obra “Almagesto”, una obra monumental que aborda la astronomía y la astrología. Esta obra abarca varios libros y es una recopilación de conocimientos astronómicos de la antigüedad, que incluye la descripción del sistema geocéntrico, donde la Tierra se considera el centro del universo, con los planetas y el Sol orbitando alrededor de ella.

Pero con respecto a las matemáticas demostró numerosos teoremas trigonométricos trabajando con el sistema sexagesimal de ángulos. Aquí enunciamos y demostramos el conocido “Teorema de Ptolomeo”. Pero antes, definamos por comodidad a que llamaremos “Cuadrilátero Cíclico”.
Definición: Un cuadrilátero decimos que es cíclico si puede inscribirse en una circunferencia, esto es si existe una circunferencia que pasa por sus cuatro vértices.
Para saber más de los cuadriláteros cíclicos, lo que no es necesario para esta entrada, puedes leer aquí.
Teorema de Ptolomeo
En un cuadrilátero cíclico ABCD, la suma de los productos de sus lados opuestos es igual al producto de sus diagonales:
\boldsymbol{\color{orange}AC·BD}=\boldsymbol{\color{#9D9DFF}AD·BC}+\boldsymbol{\color{green}AB·CD}
Parece ser que este es el enunciado que demostró Ptolomeo en su “Almagesto”. No obstante, el recíproco de este teorema también es cierto, obteniéndose una caracterización de los cuadriláteros cíclicos. Esta primera demostración hace uso de la semejanza de triángulos.
Demostración
I) Obtenemos una primera relación a partir de la semejanza de los triángulos \footnotesize \triangle ADE y \footnotesize \triangle ABC . (Figura 3, expande).
1) Partimos de un punto auxiliar \small E sobre la diagonal \small {\color{orange}BD}. De tal manera que el ángulo \small {\color{green}\lambda=\angle BAC} sea igual al ángulo \small{\color{green}\angle EAD} (Figura 1).
También podríamos decir que \small E es la intersección de la diagonal \small BD y la isogonal conjugada a la diagonal \small AC, en el ángulo \small \angle BAD.
Figura 1: \footnotesize {\color{green}\lambda=\angle BAC}={\color{green}\angle EAD}.

Expande para ver los otros dos pasos para obtener la relación \boldsymbol{\color{blue}(I)}
2) Por otro lado, los ángulos \small{\color{orange}\angle ACB} y \small{\color{orange}\angle ADB} son iguales por estar inscritos sobre la misma cuerda. (Figura 2)
3) Concluimos, por el criterio ángulo-ángulo (dos ángulos iguales), que los triángulos \small \triangle ABC y \small \triangle AED son semejantes. (Figura 3). Luego, sus lados son proporcionales:
Figura 2: \footnotesize {\color{orange}\angle ACB}={\color{orange}\angle ADB}.

Figura 3: \footnotesize \triangle ADE \simeq \triangle ABC .

\color{blue} \boldsymbol{
\boxed{ \boldsymbol{
\frac{\color{black}ED}{\color{#9D9DFF}BC} = \frac{\color{#9D9DFF}AD}{\color{orange}AC} }}
={\color{grey} \frac{AE}{AB}}
\quad \Rightarrow \quad
{\color{black}ED} = \frac{\color{#9D9DFF}AD·BC}{\color{orange}AC} \quad (I) }Observación:
Descartamos la razón en la que se encuentra el segmento \small AE porque no es un segmento de nuestro interés ni parte de él (como \small DE).
II) La segunda relación que necesitamos la obtenemos de la semejanza de los triángulos \footnotesize \triangle ABE y \footnotesize \triangle ACD . (Figura 4)
1) Los ángulos \small\angle BAE y \small\angle CAD son iguales porque ambos son suma de ángulos de amplitudes iguales (\small\color{green}\angle \lambda ) más otro ángulo común (\small\color{orange}\angle \mu). (Figura 5, expande)
Figura 4: \footnotesize \triangle ABE \simeq \triangle ACD

Expande para ver los otros dos pasos para obtener la relación \boldsymbol{\color{blue}(II)}
2) Los ángulos \small \color{purple}\angle ABD y \small\color{purple}\angle ACD son iguales por estar inscritos sobre la misma cuerda \small \color{#9D9DFF} AD. (Figura 5)
3) Entonces los triángulos \small\triangle ABE y \small\triangle ACD son semejantes, por tener dos ángulos iguales. (Figura 6). Luego, sus lados son proporcionales:
Figura 5: \footnotesize {\color{green}\angle BAD}={\color{green}\angle CAD}

Figura 6: \footnotesize {\color{green}\angle ABD}={\color{green}\angle ACD}

\color{blue} \boldsymbol{
\boxed{ \boldsymbol{
\frac{\color{black}BE}{\color{green}CD} = {\frac{\color{green}AB}{\color{orange}AC}} }}
= { \color{grey} \frac{AE}{AD}}
\quad \Rightarrow \quad
{\color{black}BE}={\color{green}\frac{AB·CD}{\color{orange}AC}} \qquad (II) }III) Sumando las expresiones (I) + (II) llegamos a:
\color{blue} \boldsymbol{
{\color{black}BE+ED} = \frac{\color{#9D9DFF}AD·BC}{\color{orange}AC} + \frac{\color{green}AB·CD}{\color{orange}AC}
\quad \Rightarrow \quad
{\color{orange}BD} = \frac{{\color{#9D9DFF}AB·CD}+{\color{green}AB·CD}}{{\color{orange}AC}} }
\\ \quad \\
\boldsymbol{
\quad \Rightarrow \quad
{\color{orange}BD·AC}={\color{#9D9DFF}AB·CD}+{\color{green}AB·CD} }
Expandir para ver Applet de Geogebra
Dos problemas cuyas soluciones se obtienen de forma inmediata aplicando el Teorema de Ptolomeo son los siguientes:
Problema 1:
Sea \small P un punto de la circunferencia circunscrita a un triángulo equilátero \small\triangle ABC. Demostrar que la distancia de \small P a uno de los vértices del triángulo es igual a la suma de las distancias a los otros dos vértices.

Expande para ver la solución:
Solución
La solución se obtiene de forma inmediata aplicando el Teorema de Ptolomeo. Basta observar que el cuadrilátero \small ABPC es cíclico y
AP·CB = AC·BP + AB·CP
Si denotamos por a los lados del triángulo \small\triangle ABC, a=\small AB=BC=AC, tenemos
a·AP=a·BP + a·CP \Rightarrow AP=BP + CP
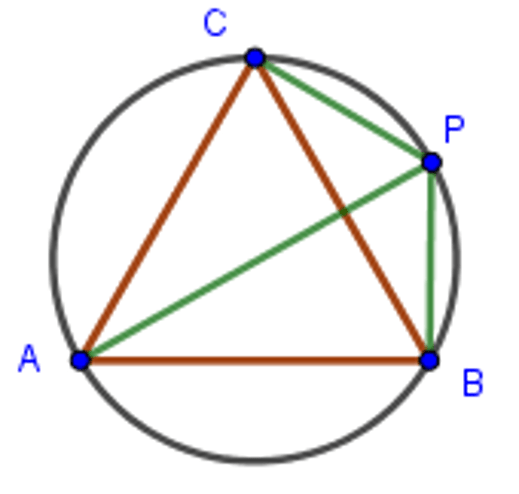
que es lo que queríamos probar. \boxdot
Problema 2:
Demostrar que la razón, \varphi, de las diagonales y los lados de un pentágono regular satisface la ecuación:
\varphi^2 - \varphi - 1=0
Esta razón es llamada “El número de oro” y vale: \varphi= \frac{1+\sqrt{5}}{2}.

Expande para ver la solución:
Solución:
Todos los polígonos regulares se pueden inscribir en una circunferencia. Por tanto el cuadrilátero BCDE es cíclico. Aplicándole el Teorema de Ptolomeo tenemos:
EC·BD=BE·CD+BC·DE
Si denotamos por d las longitudes de las diagonales y l la de los lados, tenemos
d·d=d·l+l·l \quad \Rightarrow \quad \frac{d^2}{l^2} = \frac{d·l}{l^2} + \frac{l^2}{l^2} \\ \quad \\
\left(\frac{d}{l} \right)^2 = \frac{d}{l} + 1 \quad \Rightarrow \quad \varphi^2 - \varphi -1=0. \qquad \boxdot
Desigualdad de Ptolomeo
En un cuadrilátero convexo \small ABCD, la suma de los productos de sus lados opuestos es es mayor o igual al producto de sus diagonales:
\boldsymbol{\color{orange}AC·BD}\leq\boldsymbol{\color{#9D9DFF}AD·BC}+\boldsymbol{\color{green}AB·CD}La igualdad se alcanza si y solo si el cuadrilátero es cíclico.

La demostración es totalmente análoga, en tres pasos, a la del Teorema de Ptolomeo. En el primero, al tomar el punto \small E se debe ser algo más exigente, pero en cambio la conclusión es más rápida. En el segundo paso, para la justificación de la semejanza hay que recurrir a otro argumento. Por último en el tercer paso hay que usar a mayores la desigualdad triangular.
Por otro lado, solo falta demostrar que si se cumple la igualdad el cuadrilátero es cíclico.
Demostración
I) Obtenemos una primera relación a partir de la semejanza de los triángulos \footnotesize \triangle ADE y \footnotesize \triangle ABC .
1) Partimos de un punto auxiliar \small E, tal que el ángulo \small {\color{green}\lambda=\angle BAC} sea igual al ángulo \small{\color{green}\angle EAD} (\small AE es la isogonal conjugada a \small AC en el ángulo \small \angle BAD) y tal que los triángulos \small \triangle ABC y \small \triangle AED sean semejantes, (Figura 1). Entonces:
Figura 1: \footnotesize \triangle ADE \simeq \triangle ABC

\color{blue} \boldsymbol{
\boxed{ \boldsymbol{
\frac{\color{black}ED}{\color{#9D9DFF}BC} = \frac{\color{#9D9DFF}AD}{\color{orange}AC} }}
={\color{grey} \frac{AE}{AB}}
\quad \Rightarrow \quad
{\color{black}ED} = \frac{\color{#9D9DFF}AD·BC}{\color{orange}AC} \quad (I) }II) La segunda relación la obtenemos de la semejanza de los triángulos \footnotesize \triangle ABE y \footnotesize \triangle ACD . (Figura 2)
1) Los ángulos \small\angle BAE y \small\angle CAD son iguales porque ambos son suma de ángulos de amplitudes iguales (\small\color{green}\angle \lambda ) más otro ángulo común (\small\color{orange}\angle \mu). (Figura 2)
Figura 2: \footnotesize \triangle ABE \simeq \triangle ACD

Expande para ver los otros dos pasos para obtener la relación \boldsymbol{\color{blue}(II)}
Comentario
Aquí no es valido el argumento de la igualdad de los ángulos \small \color{purple}\angle ABE y \small\color{purple}\angle ACD por estar inscritos sobre la misma cuerda, porque esto último no es cierto. (Figura 3)
2) Aquí recurrimos a una de las proporciones en (I) y que no fue usada:
\color{blue}
\boldsymbol{
\frac{\color{#9D9DFF}AD}{\color{orange}AC}
={\color{grey} \frac{AE}{AB} }
\quad \Rightarrow \quad
\boldsymbol{
\frac{\color{green}AB}{\color{orange}AC} }
= \frac{\color{grey}AE}{\color{#9D9DFF}AD}} 3) Entonces los triángulos \small\triangle ABE y \small\triangle ACD son semejantes, por criterio lado-ángulo-lado (tener un ángulo igual, con lados que los conforman proporcionales) (Figura 4). Luego todos los lados son proporcionales:
Figura 3: \footnotesize {\color{purple}\angle ABE}={\color{purple}\angle ACD}

Figura 4: \footnotesize {\color{#9D9DFF}\angle BAE}={\color{#9D9DFF}\angle CAD}

\color{blue} \boldsymbol{
\boxed{ \boldsymbol{
\frac{\color{black}BE}{\color{green}CD} = {\frac{\color{green}AB}{\color{orange}AC}} }}
= { \color{grey} \frac{AE}{AD}}
\quad \Rightarrow \quad
{\color{black}BE}={\color{green}\frac{AB·CD}{\color{orange}AC}} \qquad (II) }III) Por la desigualdad triangular \boldsymbol{ {\color{orange} BD} \leq {\color{black} BE + ED} } , (Figura 5), y la igualdad se alcanza si y solo si E está en el segmento {\color{orange} BD} .
Entonces, sumando las expresiones (I) + (II) llegamos a:

\color{blue} \boldsymbol{
{\color{orange}BD} \leq {\color{black}BE+ED} = \frac{\color{#9D9DFF}AD·BC}{\color{orange}AC} + \frac{\color{green}AB·CD}{\color{orange}AC}
\quad \Rightarrow \quad
{\color{orange}BD} \leq \frac{{\color{#9D9DFF}AB·CD}+{\color{green}AB·CD}}{{\color{orange}AC}} }
\\ \quad \\
\boldsymbol{
\quad \Rightarrow \quad
{\color{orange}BD·AC}\leq{\color{#9D9DFF}AB·CD}+{\color{green}AB·CD} }
Para terminar observemos que si E está en la diagonal, o sea se cumple la igualdad, los ángulos iguales \angle ABD y \angle ACD están apoyados sobre la misma cuerda AD . Luego C debe estar sobre la circunferencia y el cuadrilátero es cíclico. \boxdot

