El problema de descomponer en factores es equivalente a realizar divisiones y que estas sean «divisiones exactas» o de resto cero, por este motivo «Factor» es sinónimo de “Divisor”

Al dividir 20 entre 5 el resultado es 4 con resto cero, es decir la división es exacta y 5 y 4 son divisores. Además como 

20=5·4

tanto 5 como 4 son factores. En este caso los factores son números.

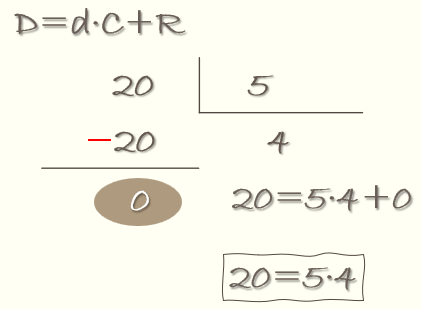
Definición de Factor:

Al dividir el polinomios D(x) = x^3 -2x^2 +2x -1 entre d(x) = x^2 - x + 1 vemos que la división es también exacta y los polinomios d(x) y C(x) = x -1 son divisores y/o factores ya que

D(x)=x^3 -2x^2 +2x -1 = (x^2 - x + 1)(x-1)

El factor de un polinomio se dice que es irreducible si no se puede descomponer en más factores y esto ocurre si los factores son polinomios de grado uno y en algunos casos polinomios de grado dos.

En este ejemplo el polinomio D(x) está descompuesto en factores irreducibles, porque d(x) y C(x) lo son.

En el caso de los números enteros no les llamamos irreducibles, sino números primos y en el ejemplo numérico que hemos puesto 20 no está descompuesto en factores primos porque 4 puede seguir descomponiendose en más factores

20=5·4=5·2·2=5·2^2

Descomponer el polinomio

P(x) = x^3−2x^2− 5x+6

en factores irreducibles.

Según la “buena noticia”, para que al dividir el polinomio P(x) , la división sea exacta los divisores posibles deben ser x\pm\textcolor{red}1, \quad x\pm\textcolor{red}2, \quad x\pm\textcolor{red}3 y x\pm\textcolor{red}6

Realizada la división entre (x - 1) vemos que esta es exacta y que

P(x) = \textcolor{blue}{(x^2 - x - 6)}(x-1)

Para seguir la descomposición en factores irreducibles debemos intentar factorizar ahora el polinomio C(x) = x^2 - x - 6 . Aquí hay dos detalles importante que destacar

Hemos comprobado que x - 1 no es factor y que x + 2 si, luego:

En realidad no es necesario que hagamos dos tablas para las descomposiciones anteriores, sino que basta prolongar la primera:

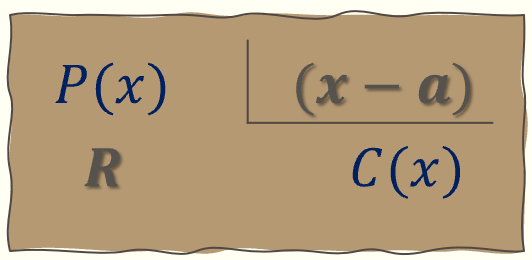
Ejemplo:

Dado el polinomio P(x) = x^2 - 3x + 5 calcula:

• 1) Por dos vías distintas el resto de la división de P(x) entre x - 2
• 2) Por dos vías distintas P(2)

Solución: 1) Primera vía: Realizamos la división por Ruffini (o Euclides) y obtenemos el resto R=3 . Segunda vía: calcular R = P(2) = 3

2) Primera vía: calcular P(2) = 3 . Segunda vía: Realizamos la división por Ruffini (o Euclides) y obtenemos el resto P(2) = R=3

Decimos que \textcolor{orange}{x = a} es raíz o cero del polinomio P(x) si al sustituir o evaluar el polinomio por \textcolor{orange}{ x = a} el resultado es cero

P(a)=0

Teorema del Factor: x = a es raíz del polinomio P(x) si y solo si (x - a) es un factor de P(x)

• a) Si x = a es raíz de P(x) entonces por el teorema del resto la división de P(x) entre (x - a) es exacta, ya que R = P(a) = 0 .

• b) Si x = a es raíz de P(x) entonces (x - a) es un factor de P(x) ya que P(x) = C(x)·(x - a) por ser la división exacta. Esto es conocido como el teorema del Factor.

• c) Si (x - a) es un factor de P(x) entonces x = a es una raíz de P(x). Porque en este caso P(x) = C(x)·(x - a) y evaluando por x = a tenemos que P(a) = C(a)·(a - a) = 0

En el polinomio del ejemplo del apartado anterior teníamos que

P(x)= x^3- 2 x^2-3x+6 = (x - 1)(x +2  )(x  - 3 )

Vamos a partir de que tenemos un polinomio \textcolor{green}{P(x)} y en consecuencia la ecuación polinomial \textcolor{green}{P(x) = 0} que podemos formar con él.

Lo primero que debemos destacar es que no debemos confundir los términos a la hora de hablar

• · El Polinomio tiene raíces
• · La ecuación tiene soluciones

Pero en ambos casos son valores de la variable, \textcolor{green}{x = a} tal que al sustituir en el polinomio el resultado es cero, \textcolor{green}{P(a) = 0}

Ejemplo: En el ejemplo del apartado anterior encontramos las raíces del polinomio

P(x)= x^3- 2 x^2-3x+6 

estas eran \textcolor{green}{ x = 1} , \textcolor{green}{ x = -2} y \textcolor{green}{ x = 3} . Entonces estos valores son también las soluciones de la ecuación

x^3- 2 x^2-3x+6 =0

En segundo lugar destacar el caso de las ecuaciones de segundo grado

ax^2 +bx+c=0

para las cuales tenemos una formula para encontrar sus soluciones

x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}

y por lo tanto estas son también las raíces del polinomio \textcolor{green}{P(x) = ax^2 +bx+c}

Ejemplo: Consideremos la ecuación de segundo grado

2x^2 -7x + 5=0

aplicando la formula para obtener sus soluciones tenemos

x=\frac{7\pm\sqrt{9}}{4}\Rightarrow \qquad x=\frac{5}{2}, x=1

y por lo tanto las raíces del polinomio P(x) = 2x^2 -7x + 5 son x=\frac{5}{2} y x=1

1) Descomponer en factores irreducibles el siguiente polinomio y dar sus raíces

P(x)= x^3- 2 x^2 - 11x + 12 

Solución: Como es un polinomio de grado 3 empezamos aplicando Ruffini, además como el término independiente es 12, los factores con los que debemos probar la división (ver apartado 1.b) son:

x\pm1, \quad  x\pm2,  \quad    x\pm3,  \quad    x\pm4,    \quad  x\pm6,  \quad  x\pm12

En principio tenemos unas cuantas posibilidades y quizás debamos probar con varios factores (esta vez la suerte nos acompañará en el primer intento)

El polinomio que debemos seguir factorizando es x^2 - x - 12 que al ser de segundo grado es mejor buscar sus raíces con la formula de la ecuación de segundo grado

x^2 - x - 12  = 0   \Rightarrow  x=\frac{-1\pm\sqrt{1+48}}{2}  = \\ \qquad \qquad \qquad \qquad \qquad=\frac{1\pm7}{2}  =\left\{ \begin{array}{l}
x=-3\\
x=4
\end{array}\right.

Entonces la descomposición es

P(x)= x^3- 2 x^2 - 11x + 12 = (x - 1)(x  + 3 )(x - 4)

y las raíces

x = 1 \qquad   x = -3 \qquad   x = 4 \qquad  

La solución al ejemplo se podrían obtener aplicando únicamente el método de Ruffini

En este caso prosiguiendo por Ruffini, después de probar nuevamente con: x - 1 \quad , con x + 1, \quad x - 2, \quad x + 2 \quad , no hemos tenido suerte (por eso a veces proseguir con Ruffini no es buena idea y es mejor ir a lo seguro con la fórmula de segundo grado).

x^3- 2 x^2 - 11x + 12 = (x - 1)(x  + 3 )(x - 4)

Donde el último factor x - 4 \quad es el último cociente que se obtiene con las divisiones por el método de Ruffini y que da lugar a la raíz

x - 4 = 0 \Rightarrow x=4

2) Descomponer en factores irreducibles el siguiente polinomio y dar sus raíces

P(x)= 9x^4 +12x^3 - 14 x^2 - 12x + 5

Aplicando Ruffini dos veces

Como el cociente de la última división es de grado dos, la mejor estrategia será resolver la correspondiente ecuación de 2do grado:

\textcolor{red}9x^2 +12x- 5 = 0 \Rightarrow x=\frac{-12\pm\sqrt{324}}{18} = \\  \qquad \qquad \qquad \qquad \qquad   = \frac{-12\pm18}{18} =\left\{ \begin{array}{l}
x=\frac{1}{3} \\
x=-\frac{5}{3}
\end{array}\right.

teniendo los dos factores irreducibles que nos faltan y quedando la descomposición

P(x) = \textcolor{red}9(x-1)(x+1)(x - \frac{1}{3})(x + \frac{5}{3})

y las raíces

x=1 \qquad  x = -1  \qquad   x= \frac{1}{3}  \qquad x =  -\frac{5}{3} 

3) Descomponer en factores irreducibles el siguiente polinomio y dar sus raíces

P(x)= x^3- 2 x^2-3x+6

Como es un polinomio de grado 3 empezamos aplicando Ruffini, probando que con los factores (x - 1), \quad (x + 1) no obtenemos resto cero, finalmente

Como el cociente de la división anterior es de grado dos, la mejor estrategia será resolver la correspondiente ecuación de 2do grado:

x^2 - 3 = 0  \quad  \Rightarrow \quad  x^2 = 3  \quad  \Rightarrow x = \pm\sqrt{3} 

obteniendo los dos factores irreducibles que nos faltan y quedando la descomposición

P(x)= x^3- 2 x^2-3x+6 = \\ \qquad \qquad \qquad= (x - 2)(x - \sqrt{3}  )(x + \sqrt{3} )

Las raíces del polinomio son

x= 2 \qquad   x = \pm \sqrt{3} 

4) Resolver la siguiente ecuación

x(x-1) (x^3- 2 x^2-3x+6) = 0

Nunca debemos desarrollar el producto anterior. El polinomio que define la ecuación está descompuesto en factores y no todos los factores son irreducibles. Las soluciones de la ecuación son las soluciones de cada uno de los factores.

Los factores irreducibles x \quad y (x + 1) que dan lugar a las soluciones

x = 0 \qquad y \qquad x=1

Las otra soluciones se obtienen de resolver la ecuación que determina el otro factor y que no es irreducible

x^3- 2 x^2-3x+6 = 0

pero esta ecuación fue resuelta en el ejercicio 3) al descomponer en factores y/o dar las raíces del polinomio que la define:

x^2 - 3 = 0  \quad  \Rightarrow \quad  x^2 = 3  \quad  \Rightarrow x = \pm\sqrt{3} 

de donde todas las soluciones son

x = 0 \qquad x=1 \qquad x = 2 \qquad x = \pm\sqrt{3}  

5) Descomponer en factores irreducibles el siguiente polinomio y dar sus raíces

P(x) = x^4-x^3+x^2-x 

Lo primero que hacemos es sacar factor común x (lo que nos lleva a que x = 0 ) es una raíz.

P(x) = x (x^3-x^2+x-1) 

Dividiendo por Ruffini (no lo hacemos aquí) obtenemos que el cociente es

(x^3-x^2+x-1):(x-1) = x^2 + 1

Sabemos que x^2 + 1 es irreducible porque la ecuación

x^2 + 1 =0

no tiene solución. Luego, la descomposición en factores del polinomio es:

P(x) = x(x-1)(x^2+1)

Sus raíces son:

x=0; \quad x=1