Ordinaria 2023.
Problema 1 de Geometría.
| Calcular la ecuación del plano \pi que es perpendicular al plano σ ≡ x+2y+3z=0 y pasa por los puntos P=(0,0,0) y Q=(0,1,1) . |
Solución:
Como los puntos P y Q están en el plano \pi entonces el vector
{\color{blue}\overrightarrow{u}} ={\color{blue}\overrightarrow{PQ}} = \left({\color{blue}0,1,1}\right)está en el el plano buscado, \pi .
Por otro lado, como los planos \sigma y \pi son perpendiculares, el vector normal de \sigma ,
{\color{red}\overrightarrow{n}} = \left({\color{red}1,2,3}\right),es paralelo a \pi .

Tenemos entonces dos vectores generadores del plano \pi , los vectores {\color{blue}\overrightarrow{u}} y {\color{red}\overrightarrow{n}} . Consideraremos además que el punto \pi está en \pi . Luego, la ecuación paramétrica del plano es:
\left\{ \begin{array}{l}
x={\color{green}0}+{\color{red}1}\alpha+{\color{blue}0}\beta\\
y={\color{green}0}+{\color{red}2}\alpha+{\color{blue}1}\beta\\
z={\color{green}0}+{\color{red}3}\alpha+{\color{blue}1}\beta
\end{array}\right.\Rightarrow\boxed{\left\{ \begin{array}{l}
x=\alpha\\
y=2\alpha+\beta\\
z=3\alpha+\beta
\end{array}, \alpha,\beta\in\mathbb{R}\right.}Expande aquí para ver más detalles y justificaciones:
Las ecuaciones paramétricas y vectoriales de un plano que pasa por un punto P_0({\color{green}x_0,y_0,z_0}) y tiene vectores generadores {\color{blue}\overrightarrow{u}} = \left({\color{blue}u_1,u_2,u_3}\right) y {\color{blue}\overrightarrow{v}} = \left({\color{blue}v_1,v_2,v_3}\right) están dadas por las relaciones:
Ecuación Vectorial
(x,y,z) = \left({\color{green} x_0,y_0,z_0}\right) + \alpha \left({\color{blue}u_1,u_2,u_3}\right) + \alpha \left({\color{blue}v_1,v_2,v_3}\right)Ecuación Paramétrica
\left\{ \begin{array}{l} x={\color{green}x_0}+\alpha{\color{blue}u_1}+\beta{\color{blue}v_1}\\
y={\color{green}y_0}+\alpha{\color{blue}u_2}+\beta{\color{blue}v_2}\\
z={\color{green}z_0}+\alpha{\color{blue}u_3} +\beta{\color{blue}v_3}
\end{array}\right.Otras Soluciones:
En este ejercicio podrían habernos pedido las ecuación general y/o segmentaria del plano. En este caso, podemos calcular un vector normal de \pi como el producto vectorial de sus vectores generadores {\color{blue}\overrightarrow{u}} y {\color{blue}\overrightarrow{v}}={\color{red}\overrightarrow{n}}:
\overrightarrow{n_{\pi}}=\overrightarrow{u}\times\overrightarrow{v}=\left|\begin{array}{ccc}
\overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k}\\
{\color{blue}0} & {\color{blue}1} & {\color{blue}1}\\
{\color{red}1} & {\color{red}2} & {\color{red}3}
\end{array}\right|=(1,1,-1)Entonces la Ecuación Normal de la recta es
(x-0)+(y-0)-(z-0)=0
y la General
\boxed{x+y-z=0}y la Ecuación General, que en este caso coincide con la Ecuación Segmentaria es
\boxed{x+y-z=0}Problema 2 de Geometría.
| Dados el plano \pi\equiv x+2y-2z=0 y la recta r\equiv\frac{x}{-2}=\frac{y-4}{2}=\frac{z-1}{1}, se pide: a) Comprobar que r es paralela a \pi. (1 punto) b) Hallar el plano \sigma, distinto de \pi y paralelo a \pi, cuya distancia a r coincide con la (distancia a) de \pi. (1 punto) |
Solución:
a) Un vector, o recta, es paralelo a un plano si y solo si es ortogonal al vector normal de este. Entonces debemos verificar que el vector normal, \overrightarrow{n_{\pi}}, de \pi y el vector director, \overrightarrow{d_{r}}, de r deben ser perpendiculares. Equivalentemente, debemos comprobar que el producto escalar de estos vectores es nulo:
\overrightarrow{n_{\pi}}=(1,2,-2)\quad\textrm{y}\quad\overrightarrow{d_{r}}=(-2,2,1)\overrightarrow{n_{\pi}}\cdot\overrightarrow{d_{r}}=1·(-2)+2·2+(-2)·1=0\Rightarrow\overrightarrow{n_{\pi}}\bot\overrightarrow{d_{r}}de donde concluimos el primer apartado.
b) El plano buscado, \sigma, al ser paralelo al plano \pi, tiene su mismo vector normal. \sigma es un plano del haz de planos paralelos a \sigma:
x+2y-2z+D=0
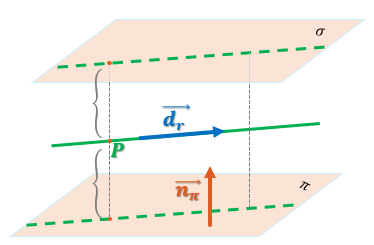
Las distancias de cualquier punto de la recta r al plano \pi son iguales, al igual que las distancias de cualquier punto de la recta r al plano \sigma. Tomemos entonces el punto P(0,-4,-1) de la recta y establezcamos esta relación:
d(P,\pi)=d(P,\sigma)\Rightarrow\frac{\left|0+2·(-4)-2·(-1)\right|}{\sqrt{1^{2}+2^{2}+(-2)^{2}}}=\frac{\left|0+2·(-4)-2·(-1)+D\right|}{\sqrt{1^{2}+2^{2}+(-2)^{2}}}de donde 10=\left|D-10\right|\Rightarrow D-10=\pm10\Rightarrow D=10\pm10\Rightarrow D=0,\:D=20 . El valor D=0 corresponde al plano \pi y el valor D=20 corresponde al plano \sigma. La Ecuación General de \sigma es:
x+2y-2z+20=0
