(1) Variables Aleatorias
(a) Definición y Clasificación
Dado un experimento aleatorio con espacio muestral E definimos como Variable Aleatoria, asociada al experimento, a una aplicación:
X:E\rightarrow\mathbb{R}
En general, no cualquier aplicación definida en un espacio muestral es considerada como una variable aleatoria, para ello, se le exige que además cumpla otras propiedades que quedan fuera del nivel de bachillerato. Pero, si te interesa, puedes echarle un ojo aquí.
Ejemplo 1:
Consideremos el experimento aleatorio que consiste en el lanzamiento de un dado cúbico (equilibrado) y observar la cara que queda hacia arriba.

El espacio muestral de este experimento es:
E=\{1,2,3,4,5,6\}Podemos definir entonces la variable aleatoria X:E\rightarrow\mathbb{R} dada por
X(k)=(-1)^k ·k^2
El rango o imagen de esta aplicación, es decir, el conjunto los resultados que se obtienen, es
Im(X)=\{x_1 = -25, x_2 = -9, x_3 = -1, x_4=4, x_5=16, x_6=36\}En la práctica, muchas veces se definen variables aleatorias, al observar una característica cuantitativa de los elementos del espacio muestral.
Ejemplo 2:
Consideremos el experimento aleatorio que consiste en seleccionar un alumno al azar de la clase 1ºD, en las que hay 16 alumnos. El espacio muestral, E, de este experimento esta compuesto por los 16 alumnos de esta clase.
Definimos la variable aleatoria X:E\rightarrow\mathbb{R} que le asigna, a cada alumno, su nota en la asignatura de Matemáticas.
Esta aplicación le asigna a un alumno el número 2 (la nota, numérica y entera del 1 al 10, de ese alumno), a un alumnos el número 3, a cinco alumnos la nota 4, a un alumno la nota 5, a cinco alumnos la nota 6, a un alumno la nota 7 y un alumno la nota 8.
La imagen o recorrido de esta variable aleatoria es:
Im(X)=\{x_1=2, x_2=3, x_3=4, x_4=5, x_5=6, x_6=7, x_7=8\}
Ejemplo 3:
Consideremos un experimento aleatorio en el que el espacio muestral está compuesto por solo dos elementos (solo hay dos resultados posibles): E=\{e,f\} (e: de éxito y f: de fracaso). Estos experimentos son llamados dicotómicos.
La variable aleatoria X:E\rightarrow\mathbb{R}
X(e)=1 \qquad X(f)=0
es conocida como Variable Aleatoria de Bernoulli.
Im(X)=\{x_1=0, x_2=1\}
Las tres variables aleatorias definidas en los ejemplos anteriores, son consideradas Variables Aleatorias Discretas, esto es así, porque el recorrido de estas aplicaciones son finitos, aunque también podrían ser “infinitos numerables”,

Un conjunto es infinito numerable si cada uno de sus elementos se puede emparejar con un números natural. Esto lo decimos en términos más matemáticos afirmando que existe una correspondencia biyectiva entre el recorrido de la variable aleatoria y los números naturales.
(b) Discretas: Función de Probabilidad (o de masa) y Función de Distribución.
Si tenemos una variable aleatoria X:E \rightarrow\mathbb{R}, a partir de ella podemos definir distintos sucesos en el espacio muestral. Denotamos por:
{\color{purple}(X=x)} := \{ \omega\in E| \, X(\omega)=x \},
\\ \quad \\
{\color{purple}(X\leq x) }:= \{ \omega\in E| \, X(\omega)\leq x \},
\\ \quad \\
{\color{purple}(X< x) }:= \{ \omega\in E| \, X(\omega) < x \}, {\color{purple}(X \geq x) }:= \{ \omega\in E| \, X(\omega) \geq x \}, \\ \quad \\
{\color{purple}(X > x)} := \{ \omega\in E| \, X(\omega) > x \}, \\ \quad \\
{\color{purple}(a< X \leq b)} := \{ \omega\in E| \, a < X(\omega) \leq b \}, ...Ejemplo 1: (Continuación)
(Ver apartado anterior)
E=\{1,2,3,4,5,6\}; \qquad X:E \rightarrow\mathbb{R},
\\ \quad \\
X(k)=(-1)^k ·k^2Im(X)=\{x_1 = -25, x_2 = -9, x_3 = -1, x_4=4, \\|x_5=16, x_6=36\}Ejemplos de sucesos:
(X=-9) = \{3\}, \qquad (X=0) = \emptyset,
\\ \quad \\
(X\leq 4) = \{ -5, 3, 1, 2 \}, \, \, (X< 4) = \{ -5, 3, 1 \}
\\ \quad \\
(X\leq 7) = \{ -5, 3, 1, 2 \}, \, \, (X< 7) = \{ -5, 3, 1 \}(X \geq -1) = \{1,2,4,6 \}, \,\, (X >-1) = \{2,3,4 \}
\\ \qquad \\
(-1< X \leq 16) = \{ 2, 4 \}, \, \, (-1\leq X \leq 16) = \{-1, 2, 4 \}
\\ \quad \\
(-1\leq X < 14) = \{ -1, 2 \}, \,\, (-1\leq X \leq14) = \{ -1, 2 \}Definición: Llamamos función de probabilidad de una variable aleatoria discreta (o función de masa) a la función p:\mathbb{R}\rightarrow\mathbb{R}
p(x)=P(X=x),\qquad \forall x\in\mathbb{R}De forma análoga, llamamos Función de Distribución de una variable aleatoria (discreta o no) a la función F:\mathbb{R}\rightarrow\mathbb{R}
F(x)=P(X\leq x),\qquad \forall x\in\mathbb{R}
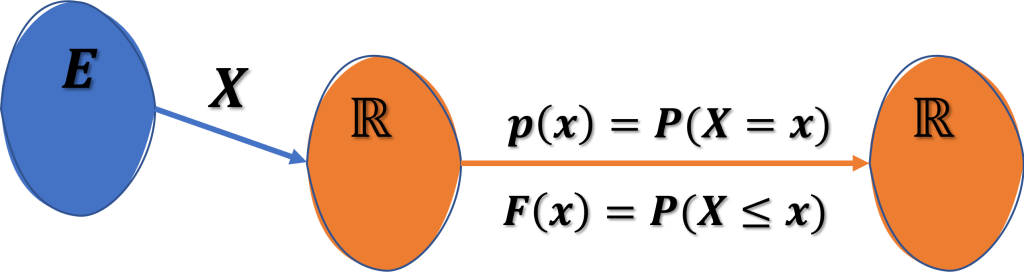
Ejemplo 1: (Continuación)
Podemos resumir la Función de Probabilidad de X en una tabla, o darla analíticamente
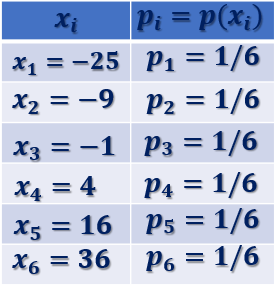

p_1 = p(x_1)=p(-25)=P(X=-25)=P(\{5\})=1/6 \\
p_2 = p(x_2)=p(-9)=P(X=-9)=P(\{3\})=1/6 \\
p_3 = p(x_3)=p(-1)=P(X=-1)=P(\{1\}=1/6 \\
p_4 = p(x_4)=p(4)=P(X=4)=P(\{2\})=1/6 \\
p_5 = p(x_5)=p(16)=P(X=16)=P(\{4\})=1/6 \\
p_6 = p(x_6)=p(36)=P(X=36)=P(\{6\})=1/6 \\ \quad \\
p(x)=P(X=x)=P(\empty)=0, \, \forall x\neq x_ip(x)=\left\{ \begin{array}{ll}
1/6 & \textrm{ si }x=1,2,3,4,5,6\\
0 & \textrm{ en otros casos}
\end{array}\right.La función de probabilidad es distinta de cero en un número finito (o infinito numerable) de valores de x y en el resto vale cero.
La Función de Distribución

F(x)=\left\{ \begin{array}{ll}
0 & \textrm{ si }x<-25\\
1/6 & \textrm{ si }-25\leq x<-9\\
1/3 & \textrm{ si }-9\leq x<-1\\
1/2 & \textrm{ si }--1\leq x<4\\
2/3 & \textrm{ si }4\leq x<16\\
5/6 & \textrm{ si }16\leq x<36\\
1 & \textrm{ si }36\leq x
\end{array}\right.{\color{purple}x < x_1=-25}, \quad F(x) = P(X\leq x)=P(\empty)=0 \qquad
\qquad \quad \\ \, \\
{\color{purple}x=x_1=-25}, \,\, F_1 = F(x_1)=P(X\leq -25)=P(\{5\})=1/6 \\ \, \\
{\color{purple}-25 \leq x < -9}, \,\, F(x)=P(X\leq x)=P(\{5\})=1/6 \qquad
\qquad \quad \\ \, \\
{\color{purple}x=x_2=-9}, \,\, F_2 = F(x_2)=P(X\leq -9)=P(\{3,5\})=2/6 =1/3 \\ \, \\
{\color{purple}-9 \leq x < -1}, \,\, F(x)=P(X\leq x)=P(\{3,5\})=1/3 \qquad \qquad \quad \\ \, \\
{\color{purple}x=x_3=-1}, \,\, F_3 = F(x_3)=P(X\leq -1)=P(\{1,3,5\})=3/6=1/2
\\ ...
La función de distribución, cuando nos movemos de izquierda a derecha, permanece constante hasta que llegamos a un nuevo x_i. En ese momento, como al suceso X\leq x_i se incorporan nuevos elementos del espacio muestral la probabilidad aumenta y la función de distribución tiene un salto (hacia arriba). La cantidad que aumenta en ese x_i es precisamente la probabilidad del conjunto de elementos que se han incorporado: p_i =P(X = x_i).


(c) Parámetros de una variable aleatoria discreta.
En “Estadística” se define una Variable Estadística Cuantitativa como una aplicación definida en una población P y que toma sus valores en los números reales, X:P \rightarrow\mathbb{R}. Pues bien, podemos decir que toda Variable Estadística Cuantitativa determina una Variable Aleatoria, de manera que ambas como funciones son la misma aplicación. La diferencia radica en que para hablar de variable aleatoria es necesario hablar de “experimento aleatorio” y al definir la variable estadística esto no se ha hecho. Basta entonces, definir el experimento aleatorio que consiste en elegir un individuo de la población al azar, en ese caso el espacio muestral es la población, E=P, y podemos tomar la variable aleatoria exactamente la misma aplicación que la variable estadística.
Ejemplo 2: (Continuación)
Consideremos el experimento aleatorio que consiste en seleccionar un alumno al azar de la clase 1ºD, en las que hay 16 alumnos…
En este caso, la población son todos los alumnos de la la clase 1ºD que coincide con el espacio muestral del experimento aleatorio. La variable estadística que a cada individuo de la población le asocia su nota, es como función, la misma que la la variable aleatoria.

En el caso de la variable estadística, hablamos de frecuencias relativas f_i: nº de veces que se repite el dato (resultado) x_i entre el total de individuos de la población. O dicho de otra forma, nº de individuos de la población que se le asigna ese resultado entre el total de individuos de la población.

En el caso de la variable aleatoria, hablamos de la función de probabilidad, p_i=P(X=x_i), que teniendo en cuenta la Regla de Laplace es: nº de individuos de la población que se le asigna ese resultado (que están en este suceso: casos favorables) entre el total de individuos de la población (casos posibles).
Existe una analogía similar entre las frecuencias relativas acumuladas en el caso de las variables estadísticas y la función de distribución en el caso de las variables aleatorias. Por lo que, podemos definir para una variable aleatoria los parámetros (poblacionales) que calculamos para las variables estadísticas.
Definición: Llamamos Valor Esperado o Media de una variable aleatoria discreta al número
\mu =E[X]=\sum_{x_{i}}x_{i}p_{i}
Definición: Llamamos Varianza de una variable aleatoria discreta al número
\sigma^2 = \sum_{x_{i}}\left(x_{i}-\mu\right)^2 p_{i}=\sum_{x_{i}}x_{i}^2p_{i} -\mu^2Llamamos Desviación Típica a la raíz cuadrada de la varianza: \sigma = \sqrt{\sigma ^2}

Ejemplo 2: (Continuación)
Consideremos el experimento aleatorio que consiste en seleccionar un alumno al azar de la clase 1ºD, en las que hay 16 alumnos…
Calcular la media, varianza y desviación típica de la variable aleatoria X:E\rightarrow\mathbb{R} que le asigna, a cada alumno, su nota en la asignatura de Matemáticas. Para ello, nos apoyaremos en dos columnas adicionales en la tabla de la función de probabilidad y distribución:

La columna de las x_ip_i se obtiene multiplicando la columna de las x_i con la de las p_i y en la ultima fila calculamos la suma de esta columna. Entonces
\mu =E[X]=\sum_{x_{i}}x_{i}p_{i} =\frac{87}{16}=5,4375De forma análoga, la columna de las x_i^2 p_i se obtiene multiplicando las columnas x_ip_i y x_i, en la ultima fila calculamos la suma de esta columna. Entonces
\sigma^2 =\sum_{x_{i}}x_{i}^2p_{i} -\mu^2 = \frac{475}{16}-\left(\frac{87}{16}\right)^2=\frac{31}{16}=1,9375\sigma=\sqrt{\sigma ^2}=\sqrt{1,9375}\approx1,392Ejemplo 1: (Continuación)
Calcular la media, varianza y desviación típica de la variable aleatoria X:E\rightarrow\mathbb{R}. Añadiendo las columnas adicionales en la tabla de la función de probabilidad y distribución:

\mu =E[X]=\sum_{x_{i}}x_{i}p_{i} =\frac{21}{6}=7,5\sigma^2 =\sum_{x_{i}}x_{i}^2p_{i} -\mu^2 = \frac{81}{6}-\left(\frac{21}{6}\right)^2=\frac{45}{6}=7,5\sigma=\sqrt{\sigma ^2}=\sqrt{7,5}\approx 2,7386(d) Propiedades de la Función de Distribución
En este apartado, F representa la función de distribución de una variable aleatoria X:E\rightarrow\mathbb{R}. Entonces
\boxed{F(\infty)=P(X\leq\infty) = P(X<\infty) = P(E) =1}El suceso (X\leq\infty) coincide con E porque cualquier \omega \in E cumple que X(\omega)<\infty.
\boxed{F(-\infty)=P(X\leq -\infty) = P(\empty) =0}El suceso (X\leq -\infty) es el suceso imposible porque cualquier \omega \in E no cumple X(\omega)\leq -\infty.
\boxed{P(a < X \leq b) =F(b) - F(a)}Para demostrar esta última propiedad observemos que el suceso (X \leq b) lo podemos escribir como unión de los sucesos, incompatibles entre si, (X \leq a) y (a < X \leq b)
(X \leq b) = (X \leq a) \cup (a < X \leq b)
por lo que P(X \leq b) = P(X \leq a) + P(a < X \leq b), y se obtiene el resultado.
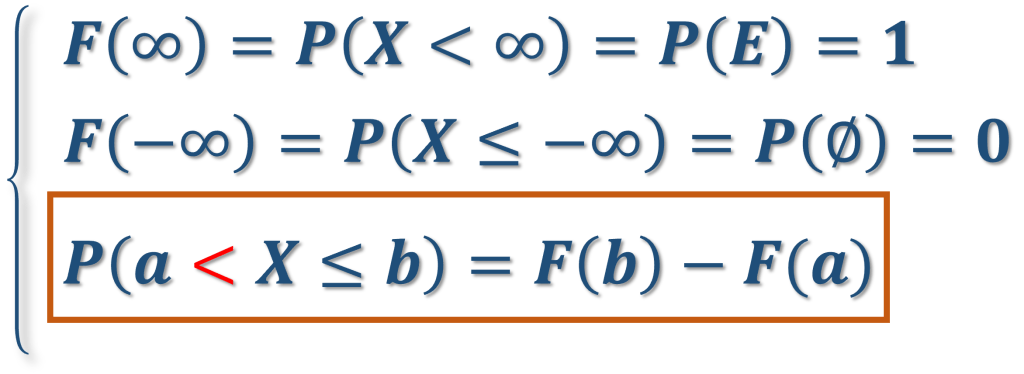
En realidad, cuando se ha escrito F(\infty) y F(-\leq\infty), se ha sido matemáticamente poco riguroso. Pero nos quedaremos con esta idea intuitiva que se ha querido transmitir.
