Extraordinaria 2023.

Problema 1 de Geometría

Dadas las rectas

r_{1}\equiv\left\{ \begin{array}{l} x=1+t\\ y=2t\\ z=-1+t \end{array}\right. \: t\in\mathbb{R}, \qquad 𝑟_{2}\equiv\frac{x-1}{3}=\frac{y}{2}=\frac{z}{2}

a) Razonar si existe un plano perpendicular a $r_{2}$ que contenga a $r_{1}$ . (1 punto)
b) Calcular la recta con vector director perpendicular a los de las rectas $r_{1}$ y $r_{2}$ y que contiene al punto $(1,0,0)$ . (1 punto)

Solución:

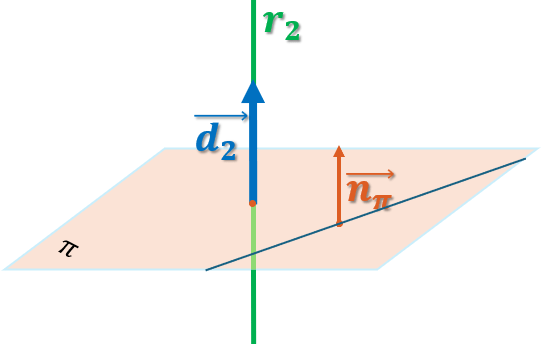
a) Todo plano que es perpendicular a la recta $r_2$ tiene como vector normal cualquier vector que sea paralelo a un vector director de $r_2$ . Más aún, toda recta contenida en dicho plano y sus vectores directores deben ser perpendiculares al vector normal de este plano, es decir al vector director de $r_2,$ $\overrightarrow{d_2}=(3,2,2)$ .

Pero

\overrightarrow{d_2}·\overrightarrow{d_1}=3·1+2·2+2·1=9 \neq0

donde $\overrightarrow{d_1}=(1,2,1)$ es el vector director de $r_1$ .

Entonces $r_1$ no puede estar incluida en ningún plano que sea perpendicular a $r_2$ , ya que su vector director no es perpendicular (y tampoco ella) al vector director de $r_2$ .

Problema adicional: Estudiar la posición relativa de

r_1

r_2

a) Descartamos que las rectas sean paralelas o coincidentes, ya que los vectores directores de estas no son proporcionales (son linealmente independientes, es decir, no tienen la misma dirección):

\frac{1}{3}\neq\frac{2}{2}\neq\frac{1}{2},\qquad rg\left(\begin{array}{ccc} 1 & 2 & 1\\ 3 & 2 & 2 \end{array}\right)=2

Por otro lado:

▪ El punto $P_1(1, 0,-1)$ de $r_1$ no está en $r_2$ . En efecto: $\frac{1-1}{3}\neq\frac{0}{2}\neq\frac{-1}{2}$ .
▪ El punto $P_2(1, 0,0)$ de $r_2$ no está en $r_1$ . En efecto: $1=1+t\Rightarrow t=0$ , se cumple que $0=2\cdot0$ , pero $0\neq -1+ 0$ .

Si las rectas se cortan, ambas deben estar en el mismo plano y los vectores directores de estas, juntos con el vector $\overrightarrow{P_{1}P_{2}}=(0,0,1)$ deben ser linealmente dependientes, pero:

\left|\begin{array}{ccc} 0 & 0 & 1\\ 1 & 2 & 1\\ 3 & 2 & 2 \end{array}\right|=\left|\begin{array}{cc} 1 & 2\\ 3 & 2 \end{array}\right|=-4\neq0

lo que significa que estos vectores son linealmente independientes. Por esta razón, estas rectas deben cruzarse y estar ambas en par de sendos planos paralelos.

b) La recta pedida tiene vector director, $\overrightarrow{d}$ , perpendicular a los vectores directores de las rectas $r_1$ y $r_2$ . Entonces podemos tomar a $\overrightarrow{d}$ como el producto vectorial de estos, es decir

\overrightarrow{d}=\overrightarrow{d_{1}}\times\overrightarrow{d_{2}}=\left|\begin{array}{ccc} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k}\\ 1 & 2 & 1\\ 3 & 2 & 2 \end{array}\right|=(2,1,-4)

La recta buscada tiene vector director $\overrightarrow{d}$ y pasa por el punto $P(1,0,0)$ , luego su ecuación continua es:

\frac{x-1}{2}=\frac{y}{1}=\frac{z}{-4}

Problema adicional: Encontrar los planos paralelos que contienen respectivamente a las rectas

r_1

r_2

La recta pedida en el apartado b) es tal que, pasa por el punto $P(1,0,0)$ y es ortogonal a un haz de planos paralelos, siendo los planos que contiene las rectas $r_{1}$ y $r_{2}$ unos de ellos.

La ecuación de este haz de planos paralelos viene dada por

2x+y-4z+D=0

donde el vector normal de estos planos es el director de la recta buscada: $\overrightarrow{n}=\overrightarrow{d} = (2,1,-4)$ .

Para determinar las ecuaciones del par de planos, $\pi_{1}$ y $\pi_{2}$ , paralelos que contienen a las rectas $r_{1}$ y $r_{2}$ , respectivamente. Debemos calcular los respectivos valores de $D$ , a partir de los puntos por donde pasan estas rectas y que estarán también en $\pi_{1}$ y $\pi_{2}$ respectivamente. En este caso podemos usar $P_1(1, 0,-1)$ y $P_2(1, 0,0)$ :

P_1: \: 2·(1)+0-4·(-1) + D_1= 0 \quad \Rightarrow \quad D_1= -6 \qquad \pi_1\equiv 2x+y-4z-6=0

P_2: \: 2·(1)+0 - 4·(0) + D_2= 0 \quad \Rightarrow \quad D_2= -2 \qquad \pi_2\equiv 2x+y-4z-2=0

Problema 2 de Geometría

Sea

r

la recta que pasa por los puntos

(1,0,-1)

(0,1,1)

,
a) Determinar el plano que contiene a la recta

r

y al punto

P(0,0,1)

. (1 punto)
b) Calcular la distancia de la recta

r

al punto

P(0,0,1)

. (1 punto)

Solución:

a) Como los puntos $A(1,0,-1)$ y $B(0,1,1)$ están en la recta $r$ y el punto $P(0,0,1)$ no lo está, tenemos que estos son tres puntos no colineales y determinan un único plano, $\pi$ . Este plano es el que nos están pidiendo.

Dos vectores generadores de $\pi$ son el vector director de la recta $r$ , $\overrightarrow{d_r} = \overrightarrow{AB} = (-1,1,2)$ , y el vector $\overrightarrow{v} = \overrightarrow{AP} = (-1,0,2)$ . Entonces la ecuación vectorial del plano es:

\pi \equiv (x, y, z) = (0, 0, 1)+ \alpha(-1,1,2)+\beta(-1,0,2), \qquad \alpha,\beta\in \mathbb{R}

No lo piden explícitamente, pero como en el próximo apartado lo usaremos, calculamos también la ecuación general de $\pi$ . Su vector normal es

\overrightarrow{n_{\pi}} = \overrightarrow{d_{r}} \times \overrightarrow{AP} = \left|\begin{array}{ccc} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k}\\ -1 & 1 & 2\\ -1 & 0 & 2 \end{array}\right|=(2,0,1) \qquad \Rightarrow \qquad 2(x-0)-0(y-0)+1·(z-1)=0

donde la ecuación general queda: $2x+z-1=0$

b) La distancia de $P$ a $r$ la podemos calcular mediante la relación (ver aquí justificación de la relación)

d(P,r)=\frac{\left| \overrightarrow{d_{r}}\times\overrightarrow{AP}\right|}{\left|\overrightarrow{d_{r}}\right|} \qquad \Rightarrow \qquad d(P,r)=\frac{\left|(2,0,1)\right|}{\left|(-1,1,2)\right|}=\frac{\sqrt{5}}{\sqrt{6}}=\frac{\sqrt{30}}{6}u

Otra vía, buscando la proyección del punto en la recta

Buscamos la proyección ortogonal de $P$ en $r$ , $Q$ .

1) Determinamos el plano, $\pi,$ ortogonal a $r$ que pasa por $P$ ( $\overrightarrow{n_{\pi}}=\overrightarrow{d_{r}}$ ):

\pi: -x+y+2z+D=0, P\in\pi \Rightarrow \\ \, \\ \Rightarrow 2+D=0 \Rightarrow D=-2 \Rightarrow \\ \, \\ \pi: -x+y+2z-2=0

2) $Q$ es el punto de corte de $\pi$ y $r$ :

r:\left\{ \begin{array}{l} x=1-t\\ y=t\\ z=-1+2t \end{array}\right. \quad Q(1-t,t,-1+2t)\in\pi \\ \, \\ -(1-t)+t+2(-1+2t)-2=0 \Rightarrow \\ 6t-5=0 \Rightarrow t=\frac{5}{6} \Rightarrow Q(1/6,5,6,-1/3)

3) $d(P,r)=d(p,Q)$

d(P,r)=d(p,Q) = \sqrt{ \left( \frac{1}{6} \right)^2 + \left( \frac{5}{6} \right)^2 + \left( \frac{-1}{3} \right)^2} = \frac{\sqrt{30}}{6}u