Extraordinaria 2022.

Problema 1 de Probabilidad

Entre los participantes de un torneo internacional de ajedrez:
El 28% de ellos son rusos, de los cuales las tres cuartas partes son grandes maestros.
El 24% son estadounidenses y entre ellos la mitad son grandes maestros.
Mientras que, el 48% son del resto del mundo, de los cuales un tercio son grandes maestros.
Considerando los sucesos: $R=$ “ser ruso”, $E=$ “ser estadounidense”, $M=$ “no ser ruso ni estadounidense” y $GM=$ “ser gran maestro”.
a) Indique cuáles son los valores de $P(GM|R)$ , $P(GM|E)$ y $P(GM|M)$ .
b) Calcule la probabilidad de que al elegir al azar a uno de los participantes en el torneo, sea un gran maestro.
c) Si se elige al azar a uno de los grandes maestros del torneo, ¿cuál es la probabilidad de que sea ruso?

Comentarios: Tal y como comentamos en la “EBAU 2023“, antes de enunciar el apartado a), debería haber sido definido el experimento aleatorio, lo cual fue hecho en el apartado b). “Si se selecciona un participante al azar ”

Calcule la probabilidad de que el jugador elegido al azar sea un gran maestro.
Sabiendo que el jugador elegido es un “gran maestro”, ¿cuál es la probabilidad de que sea ruso?

Solución

Los porcentajes dados nos permiten conocer las probabilidades de algunos de los sucesos:

P(R)=0,28 \quad P(E) = 0,24 \quad P(M) = 0,48

(C1) Observemos que $M=\overline{E}\cap\overline{R}$ y es lógico suponer que cada jugador solo representará a un solo país. Entonces $M, R$ y $E$ son incompatibles dos a dos. Además la unión de estos tres sucesos es todo el espacio muestral.

a) Por otro lado también podemos inferir del enunciado las probabilidades de algunos sucesos condicionados, que son los pedidos en este apartado,

P(GM|R)=3/4 \quad P(GM|E)=1/2 \quad P(GM|M)=1/3

b) Para el calculo de la probabilidad pedida en este apartado aplicaremos el Teorema de las Probabilidades Totales, esto lo podemos hacer porque se cumplen las premisas (C1).

P(GM)=P(GM|R)P(R)+P(GM|E)P(E)+P(GM|M)P(M) = \qquad \quad \\ \qquad \quad = 0,28·3/4 + 0,24·1/2 +0,48·1/3 = 0,21+0,12+0,16=0,49

c) En este último apartado (y como es usual en este tipo de preguntas) aplicamos el Teorema de Bayes:

P(R|GM) = \frac{P(GM|R)P(R)}{P(GM)} = \frac{0,28·3/4}{0,49} = \frac{0,21}{0,49}=\frac{3}{7}

Problema 2 de Probabilidad

La variable agudeza visual de una población se ajusta a una distribución normal de media 2 cpg (ciclos por segundo) y desviación típica 1 cpg. A los individuos con una agudeza visual inferior a 1.1 cpg se les considera con “problemas visuales graves”.
a) ¿Qué porcentaje de la población tiene “problemas visuales graves”?
b) ¿Qué porcentaje de la población tiene una agudeza visual entre 2 y 2.9 cpg?

Solución

Denotemos por:

X

: la agudeza visual de los individuos de una población.

Entonces por hipótesis, $X\sim N(2,1)$ .

a) Para calcular el porcentaje pedido, calcularemos la probabilidad de que un individuo de la población (elegido al azar) tenga problema de visión.

También, por hipótesis, este individuo tendrá problemas de visión si: $X\leq1,1$ . Por lo que la probabilidad de que esto ocurra es $P(X\leq1,1)$ . Para calcularla, como los valores de los que disponemos (en la tabla) son los de una distribución $Z\sim N(0,1)$ , tendremos que tipificar.

Z=\frac{X-2}{1} \sim N(0,1)

P(X\leq1,1)=P\left(Z\leq\frac{1,1-2}{1}\right)=P\left(Z\leq-0,9\right)

Como $z_0 = -0,9$ es negativo, y no aparece en la tabla, tenemos que recurrir a las propiedades de la función de densidad de esta variable aleatoria, por ejemplo que es simétrica:

P(X\leq1,1)=P\left(Z\leq-0,9\right) = P(Z \geq 0,9 ) = \\ = 1-P(Z < 0,9) =1- P(Z \leq 0,9)

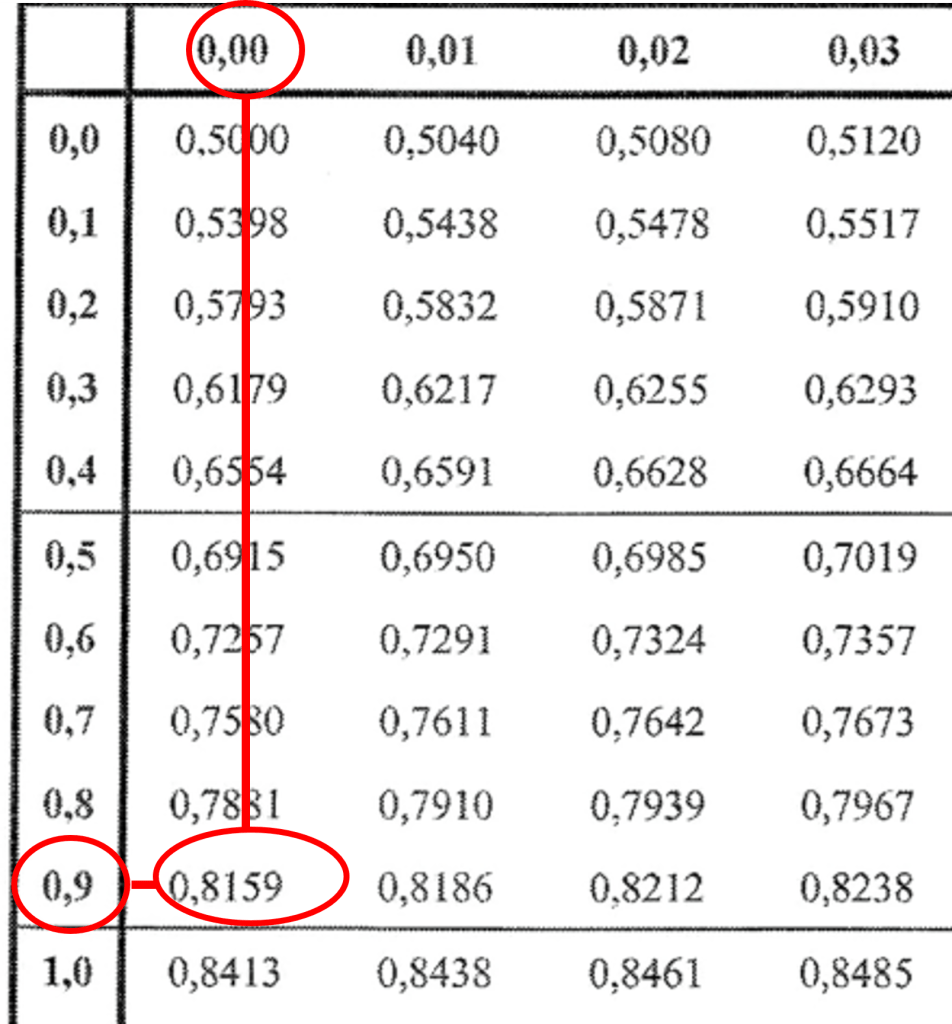
P(X\leq1,1)=1- P(Z \leq 0,9) = \qquad \qquad \\ = 1 - 0,8159 = 0,1841

Por otro lado, si entendemos la probabilidad en el sentido clásico, es decir, a partir de la Regla de Laplace, esta probabilidad nos daría la razón de la población que tiene problemas de visión, por lo que:

Respuesta: El porcentaje de la población con problemas de visión es del 18,41%.

b) Este apartado es similar al anterior. Para calcular el porcentaje pedido, calcularemos la probabilidad de que un individuo de la población (elegido al azar) tenga la agudeza visual en el rango pedido. Entonces:

P(2 \leq X \leq2,9)=P\left(\frac{2-2}{1} \leq Z \leq \frac{2,9-2}{1} \right) = P(0 \leq Z \leq 0,9) = \\ = P(Z \leq 0,9) - P(Z \leq 0) = 0,8159 - 0,5 = 0,3159

Respuesta: El porcentaje de la población que tiene agudeza visual es del 31,59%.