Extraordinaria 2022.

Problema 1 de Análisis

Dada la función

f(x)=\frac{x^2}{2 - x}

, se pide:
a) Encuentre su dominio y calcule sus asíntotas, si las tiene. (1 punto)
b) Determine los intervalos de crecimiento y decrecimiento y los máximos y mínimos relativos, si los tiene. (1 punto)

Solución

a) $\circledcirc$ El dominio de esta función es: $Dom(f)=\mathbb{R}-{2}$ , donde es continua y derivable por ser cociente de funciones polinómicas y el denominador se anula en $2-x=0 \Rightarrow x=2$ .

\circledcirc

La función puede tener una asíntota vertical en

x=2

(alguno de los límites laterales debe ser

+\infty

-\infty

\nexists \quad \underset{x\rightarrow2}{\lim}f(x) = \underset{x\rightarrow2}{\lim}\frac{x^2}{2-x} = \underset{Indet.}{\left(\frac{2}{0}\right)}

\underset{x\rightarrow2^+}{\lim}f(x) = \underset{x\rightarrow2^+}{\lim}\frac{x^2}{2-x} = -\infty \quad (f(2,1)<0) \\ \quad \\ \underset{x\rightarrow2^-}{\lim}f(x) = \underset{x\rightarrow2^-}{\lim}\frac{x^2}{2-x} = \infty \quad (f(1,9)>0)

entonces $x=2$ es una asíntota vertical.

\circledcirc

Para las asíntotas horizontales debemos analizar lo que ocurre cuando

x

tiende a

+\infty

-\infty

, es decir el comportamiento de la gráfica para los valores de

x

“suficientemente” grandes:

\underset{x\rightarrow\infty}{\lim}f(x) = \underset{x\rightarrow\infty}{\lim}\frac{x^2}{2 - x}= \underset{Indet.}{\left(\frac{\infty}{\infty}\right)}\overset{L'Hopit.}{=} \\ =\underset{x\rightarrow\infty}{\lim}\frac{2x}{-1}=-\infty

\underset{x\rightarrow-\infty}{\lim}f(x) = \underset{x\rightarrow-\infty}{\lim}\frac{x^2}{2 - x}= \underset{Indet.}{\left(\frac{\infty}{\infty}\right)}\overset{L'Hopit.}{=} \\ =\underset{x\rightarrow-\infty}{\lim}\frac{2x}{-1}=\infty

entonces no hay asíntotas horizontales.

Para el estudio de las asíntotas oblicuas, analizamos los dos limites, en $+\infty$ y $-\infty$ conjuntamente:

m=\underset{x\rightarrow\pm\infty}{\lim}\frac{f(x)}{x} = \underset{x\rightarrow\pm\infty}{\lim}\frac{\frac{x^2}{2 - x}}{x}=\underset{x\rightarrow\pm\infty}{\lim}\frac{x^2}{2x-x^2}=\\ \, \\ = \underset{x\rightarrow\pm\infty}{\lim}\frac{x^2}{-x^2} =-1

n=\underset{x\rightarrow\pm\infty}{\lim}\left[ f(x) -mx \right] = \underset{x\rightarrow\pm\infty}{\lim}\left[ \frac{x^2}{2 - x} +x \right] = \\ \, \\ = \underset{x\rightarrow\pm\infty}{\lim}\left[ \frac{x^2+2x-x^2}{2 - x} \right] = \underset{x\rightarrow\pm\infty}{\lim}\left[ \frac{2x}{ - x} \right] =-2

entonces concluimos que ${\color{darkred}y=mx+n=-x-2}$ es una asíntota oblicua en $+\infty$ y en $-\infty$ .

b) Para el estudio de la monotonía y los extremos de la función debemos analizar la primera derivada de la función:

f'(x)=\frac{2x(2-x)-x^2(-1)}{(2-x)^2}=\frac{-x^2+4x}{(2-x)^2}

f

no es derivable en

x=2

Puntos críticos $f'(x)=0$

f'(x)=0 \Rightarrow -x^2+4x=x(-x+4)=0 \Rightarrow \\ \, \\ \Rightarrow \left\{ \begin{array}{l} x=0\\ x=4 \end{array}\right.

{\color{darkorange}x=-1 \in (-\infty,0)} \\ f'(-1)= -5/9 < 0 \\ \quad \\ {\color{darkorange}x=1 \in (0,2)} \\ f'(1)= 3 >0

{\color{darkorange}x=3 \in (2,4)} \\ f'(3)= 3 >0 \\ \quad \\ {\color{darkorange}x=5 \in (4,\infty)} \\ f'(5)= -5/9 <0

Entonces $f$ es creciente en $(0,2)$ y $(2,4)$ .

f

es decreciente en

(-\infty,0)

(4,\infty)

Mínimo relativo en el punto $(0,0)$ , $f(0)=0$ .

Máximo relativo en el punto $(4,-8)$ , $f(4)=-8$ .

Expande para ver otros detalles que no son pedidos en el ejercicio (como esbozo de la grafica)

f''(x)=\frac{-8}{(x-2)^3} \qquad \qquad \\ \, \\\qquad f''(x)>0, \forall x\in(-\infty,2) \quad \\ f''(x)<0, \forall x\in(2, \infty)

Problema 2 de Análisis

a) Calcule

\underset{x\rightarrow0}{\lim}\frac{\ln(1+x)}{e^{x}-1} \qquad

. (1 punto)
b) Estudiando previamente el signo de la función en el intervalo

[0,3]

, hállese el área limitada por la gráfica de la función

f(x)=x^3 - 9x

y el eje de abscisas, cuando

x

varía en el intervalo

[0,3]

. (1 punto)

Solución

a) Calculamos el límite:

\underset{x\rightarrow0}{\lim}\frac{\ln(1+x)}{e^{x}-1}=\underset{Indet.}{\left(\frac{0}{0}\right)}\overset{L'Hopit.}{=}\underset{x\rightarrow0}{\lim}\frac{\frac{1}{1+x}}{e^{x}}=\frac{1}{1}=1

b) La función $f(x)=x^3 - 9x$ es continua en $\mathbb{R}$ y en particular en $[0,3]$ por ser polinómica. Por lo que esta función solo puede cambiar de signo en los valores de $x$ donde se anula:

f(x)=x^3 - 9x =x(x^2 - 9)=0 \Rightarrow \\ \, \\ \Rightarrow \left\{ \begin{array}{l} x=-3\\ x=0\\ x=3 \end{array}\right.

Como no se anula en ningún valor de $x\in(0,3)$ , la función mantiene el signo en todo este intervalo abierto. Como $f(1)=-8<0$ , entonces $f(x)<0, \forall x\in(0,3)$ . $f(0)=f(3)=0$ .

El área pedida es:

Área = \left|\int_{0}^{3} x^3 - 9x\, dx\right| = -\left( \left.\frac{x^4}{4}-9\frac{x^2}{2}\right]_{0}^{3} \right) = \\ \, \\ -\left[ \left(\frac{81}{4}-\frac{9}{2}\right) - 0 \right] =\frac{81}{4}u^2

Figura: Wolfram Alpha

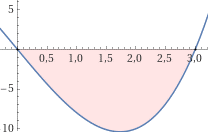
Área = \left|\int_{0}^{3} x^3 - 9x\, dx\right| = -\left( \left.\frac{x^4}{4}-9\frac{x^2}{2}\right]_{0}^{3} \right) = \\ \, \\ -\left[ \left(\frac{81}{4}-\frac{9}{2}\right) - 0 \right] =\frac{81}{4}u^2

Problema 3 de Análisis

a) Enuncie el Teorema de Bolzano. (1 punto)
b) Averigüe si la función

f(x)=x+\textrm{sen}(x) - 2

se anula en algún punto del intervalo

[0,\frac{\pi}{2}]

. (1 punto)

Solución

a) Teorema de Bolzano

Sea $f$ una función continua en el intervalo cerrado $[a,b]$ . Si $f$ toma valores de distintos signos en los extremos del intervalo, $f(a)\cdotf(b)<0$ , entonces existe $c\in(a,b)$ tal que $f(c)=0$ .

b) La función $f(x)=x+\textrm{sen}(x) - 2$ es continua en todo $\mathbb{R}$ y en particular en $[0,\frac{\pi}{2}]$ por ser suma de una función afín y la función seno. Además

f(0)=0+\textrm{sen}(0) - 2=-2<0, \\ \, \\ f\left(\frac{\pi}{2}\right)=\frac{\pi}{2}+\textrm{sen}\left(\frac{\pi}{2}\right) - 2 \approx 0,57 >0

entonces por el Teorema de Bolzano existe $c\in[0,\frac{\pi}{2}]$ tal que $f(c)=0$ .

Problema 4 de Análisis

a) Estudie el signo de la función

f(x)=x^3 -4x^2 +3x

en el intervalo

[0,2]

. (0,5 puntos)
b) Calcule el área limitada por la gráfica de la función

f(x)=x^3 -4x^2 +3x

y el eje de abscisas en el intervalo [0,2]. (1,5 puntos)

Solución

a) La función $f(x)$ es continua en todo $\mathbb{R}$ y en particular en $[0,2]$ por ser polinómica. Por lo que esta función solo puede cambiar de signo en los valores de $x$ donde se anula:

f(x)=x^3 - 4x^2+3x =x(x^2 - 4x+3)=0 \Rightarrow \\ \, \\ \Rightarrow \left\{ \begin{array}{l} x=0\\ x=1\\ x=3 \end{array}\right.

f

se anula en

x=0\in[0,2]

y en

x=1\in(0,2)

0,5\in(0,1),\quad f(0,5) =0,625 >0 \\ f(x) >0, \forall x\in(0,1) \\ \, \\ 1,5\in(1,2),\quad f(0,5) =-1,125 <0, \\ f(x) <0, \forall x\in(1,2)

b) Para el cálculo del área debemos calcular integrales definidas en dos intervalos

Área = \left|\int_{0}^{1}x^3 - 4x^2+3x \, dx\right| + \left|\int_{1}^{2}x^3 - 4x^2+3x \, dx\right| = \\ \, \\ =\left| \left.\frac{x^4}{4}-\frac{4x^3}{3}+\frac{3x^2}{2}\right]_{0}^{1} \right| + \left| \left.\frac{x^4}{4}-\frac{4x^3}{3}+\frac{3x^2}{2}\right]_{1}^{2} \right| = \\ \, \\ = \left| \left(\frac{1}{4}-\frac{4}{3}+\frac{3}{2}\right) - 0 \right| + \left| \left(\frac{16}{4}-\frac{32}{3}+\frac{12}{2}\right) - \left(\frac{1}{4}-\frac{4}{3}+\frac{3}{2}\right) \right| = \\ \, \\ =\frac{5}{12}+\frac{13}{12}=\frac{3}{2}u^2

Figura: Wolfram Alpha