Ordinaria 2021.
Problema 1 de Análisis
| Representar la función f(x)=e^{(x^2)}, determinando antes sus intervalos de crecimiento y decrecimiento, sus extremos relativos, sus intervalos de concavidad y convexidad y sus asíntotas. |
Solución
Dominio y Asíntotas
\circledcirc El dominio de esta función es: Dom(f)=\mathbb{R}, donde es continua y derivable por ser composición de una exponencial y una cuadrática. \circledcirc La función no tiene asíntotas verticales, pues estas hay que buscarlas en valores x=a, donde alguno de los límites laterales debe ser +\infty o -\infty y esta función es continua en \mathbb{R}. \circledcirc Para las asíntotas horizontales y/o oblicuas debemos analizar lo que ocurre cuando x tiende a +\infty o -\infty, es decir el comportamiento de la gráfica para los valores de x “suficientemente” grandes:\underset{x\rightarrow\infty}{\lim}f(x) = \underset{x\rightarrow\infty}{\lim}e^{(x^2)}= \infty \\ \qquad \\
\underset{x\rightarrow\infty}{\lim}\frac{f(x)}{x} = \underset{x\rightarrow\infty}{\lim}\frac{e^{(x^2)}}{x}=\underset{Indet.}{\left(\frac{\infty}{\infty}\right)}\overset{L'Hopit.}{=}\\ \, \\ =\underset{x\rightarrow\infty}{\lim}2xe^{(x^2)}=\infty
Nota: m=\underset{x\rightarrow\infty}{\lim}\frac{f(x)}{x}, es la pendiente de la asíntota oblicua, si este límite es fínito.
\underset{x\rightarrow-\infty}{\lim}f(x) = \underset{x\rightarrow-\infty}{\lim}e^{(x^2)}= \infty
\\ \quad \\
\underset{x\rightarrow-\infty}{\lim}\frac{f(x)}{x} = \underset{x\rightarrow-\infty}{\lim}\frac{e^{(x^2)}}{x}=\underset{Indet.}{\left(\frac{\infty}{\infty}\right)}\overset{L'Hopit.}{=}\\ \, \\ =\underset{x\rightarrow-\infty}{\lim}2xe^{(x^2)}=-\infty entonces concluimos que la función no tiene asíntotas horizontales ni oblicuas.
Monotonía
\circledcirc Para el estudio de la monotonía y los puntos extremos analicemos la primera derivada de la función:f'(x)=2xe^{(x^2)} =0 \Rightarrow x=0
\\ \, \\
{\color{darkorange}x=-1 \in (-\infty,0)} \\
f'(-1)= -2e < 0 \\ \quad \\
{\color{darkorange}x=1 \in (0,\infty)} \\
f'(1)= 2e >0

Entonces concluimos que f(x) es decreciente en el intervalo (-\infty, 0) y creciente en el intervalo (0, \infty). A partir de aquí, también concluimos que tiene un mínimo relativo y absoluto en el punto (0,1), f(0)=e^{0}=1. Y no tiene máximos relativos.
Curvatura:
\circledcirc Para el estudio de la curvatura y los puntos de inflexión analizamos la segunda derivada de la función:f''(x)=2e^{(x^2)} + 4x^2e^{(x^2)}=2(2x^2+1)e^{(x^2)}>0 \qquad \qquad Entonces concluimos que f(x) es cóncava en todo \mathbb{R} y no tiene puntos de inflexión.
Esbozo de la función
Figura: Wolfram Alpha

Figura: Geogebra

Problema 2 de Análisis
| Calcula \underset{x\rightarrow0}{\lim}\frac{e^{x}-x-\cos(3x)}{\textrm{sen}^{2}x} |
Solución
\underset{x\rightarrow0}{\lim}\frac{e^{x}-x-\cos(3x)}{\textrm{sen}^{2}x}=\underset{Indet.}{\left(\frac{0}{0}\right)}\overset{L'Hopit.}{=}\underset{x\rightarrow0}{\lim}\frac{e^{x}-1+3\textrm{sen}(3x)}{\textrm{sen}(2x)}=\\ \, \\
=\underset{Indet.}{\left(\frac{0}{0}\right)}\overset{L'Hopit.}{=}\underset{x\rightarrow0}{\lim}\frac{e^{x}+9\cos3x}{2\cos(2x)}=\frac{10}{2}=5Problema 3 de Análisis
| a) Dadas las funciones f(x)=x^2, g(x)=-x^2 + 8, hallar los valores de x\in\mathbb{R} para los que g(x)\geq f(x) (0,5 puntos) b) Calcular el área limitada por las gráficas de las funciones f(x) y g(x). (1,5 puntos) |
Solución
a) Tomemos la función auxiliar h(x) = g(x) - f(x), entonces h(x) \geq 0 \Leftrightarrow g(x) \geq f(x). Analicemos el signo de la función h(x)
h(x) =-x^2 + 8 - x^2 =-2x^2 +8=0 \Rightarrow \\ \, \\ \Rightarrow x=\pm2
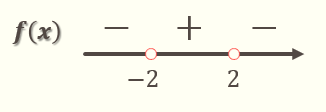
-3\in(-\infty,-2), \, h(-3)=-10<0 \\ 0\in(-2,2), \, h(0)=8>0 \\ 3\in(2, \infty), \, h(3)=-10<0
entonces h(x) = g(x) \geq f(x) \Leftrightarrow x\in [-2, 2].
b) Las funciones g(x) y f(x) se cortan en los puntos de abscisas x=\pm2 y es entre estos puntos donde las gráficas de estas dos funciones encierran el área pedida, entonces
Área = \left| \intop_{-2}^{2}g(x) - f(x)dx \right|= \intop_{-2}^{2}-2x^2 +8 dx en la segunda igualdad hemos omitido el valor absoluto, porque en este intervalo el integrando es positivo:
Área = \left. \frac{-2x^3}{3} + 8x\right]^2_{-2}= \left( \frac{-16}{3} + 16\right) - \left( \frac{16}{3} - 16\right) = \frac{64}{3} u^2 Problema 4 de Análisis
| Hallar los valores de a, b y c para los cuales el polinomio P(x)=ax^2 + bx +c cumple las siguientes condiciones: 1) P(0)=1 2) La pendiente de la recta tangente a la gráfica de P(x) en x=0 es m=1. 3) \intop_{0}^{2}P(x)dx=12 (2 puntos) |
Solución
Exijamos una a una las condiciones que debe cumplir este polinomio de segundo grado:
1) \quad 1=P(0)=c \Rightarrow c=1
Para la segunda condición, recurrimos a la interpretación geométrica de la derivada, entonces:
P'(x) =2ax+b \\ \ \\ 2) \quad 1=m=P'(0)=b \Rightarrow b=1 \\ \, \\
De estas dos condiciones tenemos que
P(x)=ax^2 +x +1
entonces la tercer condición nos queda
3) \quad 12=\intop_{0}^{2}P(x)dx=\intop_{0}^{2}ax^2 +x+1dx =
\\= \left. \frac{ax^3 }{3}+ \frac{x^2}{2}+x\right]^2_0 = \\ =\left(\frac{8a }{3}+ 2+2\right) -0= \frac{8a }{3}+ 4 \quad \Rightarrow \\ \, \\
12=\frac{8a }{3}+ 4 \quad \Rightarrow \quad a=3 Entonces a=3, b=1 y c=1.
