Relación entre Rectas y Rectas

(1) Distancia entre dos Rectas

Definición: Las distancia entre dos rectas es la menor de las distancias de un punto de una recta a otro punto de la otra recta.

Caso 1: Si dos rectas r y s son secantes, el punto de intersección, Q, cuenta como punto de r y como punto de s, entonces d(r,s)=d(Q,Q)=0.

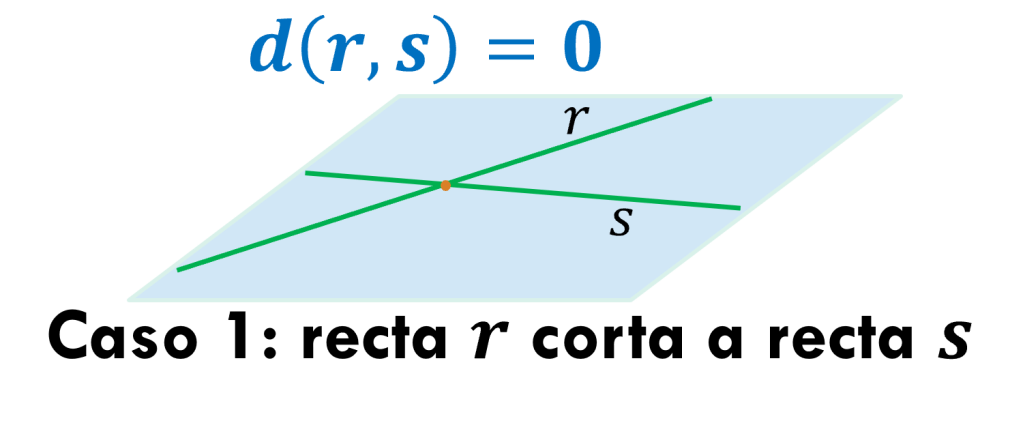
Tanto las rectas secantes como las paralelas y las coincidentes están contenidas en un mismo plano.

Caso 2: Si las dos rectas r y s son paralelas las distancias de cualquier punto de una de ellas a la otra recta son iguales

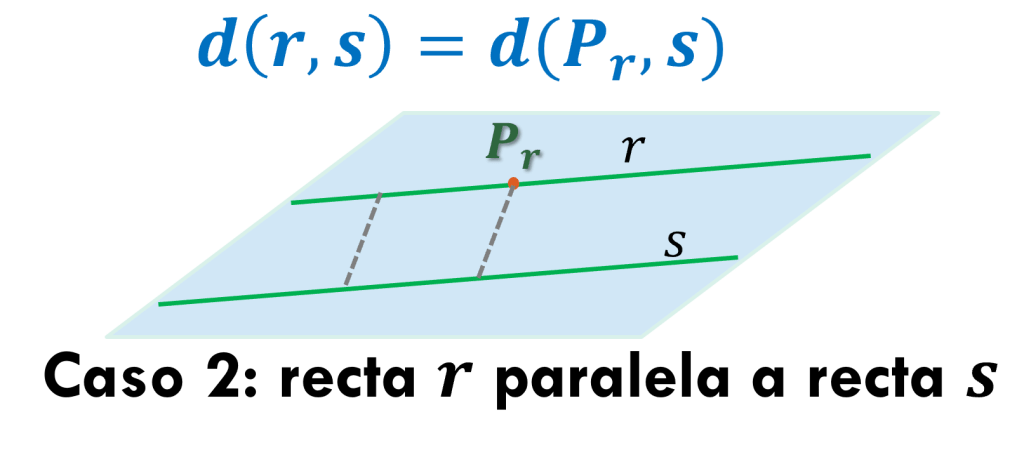
podemos observar que dos puntos de r y sus proyecciones ortogonales en s forman un rectángulo. Por esta razón, las distancias de estos puntos a sus respectivas proyecciones ortogonales son iguales.

Caso 3: En el caso de dos rectas que se cruzan, r y s, existen un par de planos paralelos que contienen a cada una de las rectas. La distancia entre estos planos coincide con la distancias entre las rectas y con la altura del paralelepípedo formado por los vectores directores de las rectas y el vector formado por cualquier par de puntos, uno de cada recta. Por otro lado, el volumen del paralelepípedo es área de la base por la altura (distancia entre los planos).

Del razonamiento anterior se obtiene: