Concepto de Matriz. Elementos y Notaciones.

Concepto y definición

¿Cómo definir una matriz? Podemos hacerlo diciendo que una matriz es una tabla de valores organizados en filas y columnas. Pero, ¿qué es una tabla de valores? Estamos ahora nuevamente en el punto de partida. No obstante, es la mejor idea intuitiva que podemos tener sobre las matrices. Y por si esto fuera poco, puede ser uno de los conceptos matemáticos para los que tenemos una idea intuitiva tan clara.

Tablilla babilónica de barro, Plimpton-322 (1500a.c), muestra 60 números en 15 filas y 4 columnas. Matriz $15\times 4.$

Tabla manuscrita comparativa, según un análisis daliniano (1947),… su visión de otros artistas. Matriz $11\times 8.$

Definición: Matriz: Objeto matemático:

Compuesto por $\boldsymbol{\color{red}{k=m·n}}$ elementos, $\boldsymbol{k,n \in \mathbb{N}}$ , que pueden ser números o cualquier otro tipo de objetos matemáticos o elementos de cualquier conjunto.
Cada elemento tiene dos características:

Nº de fila: número comprendido entre $1$ y $n$ , incusives.

Nº de columna: número comprendido entre $1$ y $m$ , inclusives.

En este caso decimos que la matriz tiene dimensión $\boldsymbol{\color{red}{m\times n}}$ . Y utilizamos la expresión: “que sus elementos están dispuestos en filas y columnas“.

El conjunto de matrices de dimensión $\boldsymbol{m\times n}$ y con elementos de un conjunto $X$ lo denotaremos por $\boldsymbol{M_{m\times n}(X)}$ .

En lo que sigue al conjunto de matrices de números reales lo denotaremos simplemente por $\boldsymbol{M_{m\times n}}$ o $\mathbb{R}^{m\times n}$ .

Cuando escribimos una matriz sus elementos son usualmente escritos entre paréntesis. Matriz genérica de dimensión $\color{red}{m\times n}:$

\small A=\left(\begin{array}{lccccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1n-1} & a_{1n}\\ a_{21} & a_{22} & a_{23} & \ldots & a_{2n-1} & a_{2n}\\ a_{31} & a_{32} & a_{33} & \ldots & a_{3n-1} & a_{3n}\\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ a_{m1} & a_{m2} & a_{m3} & \ldots & a_{mn-1} & a_{mn} \end{array}\right)

A esta matriz la hemos nombrado por $A$ pero a sus elementos en en minúscula, haciendo visible las dos características de los elementos de la matriz: la fila y la columna.

Notaciones.

Expande para ver una definición formal de matriz

Casi todas las principales ramas y/o teorías matemáticas actuales están desarrolladas a partir del sistema axiomático ZF, que es como es llamado al conjunto de axiomas asumidos para la teoría de conjuntos. Una de las primeras “definiciones formales” que se puede obtener a partir de estos axiomas es la de función. Las funciones son utilizadas a su vez para “definir formalmente” muchos de los objetos matemáticos.

Denotemos por $[n]$ al conjunto de los números naturales desde 1 hasta n, ambos inclusive:

[n]=\{1,2,...,n\}

Definición: Una matriz de elementos de $X$ y dimensión $m\times n$ es una aplicación:

A\equiv a:[m]\times[n] \rightarrow X \qquad \qquad \qquad \\ (i,j) \rightarrow a(i,j)=a_{ij}

Al destacar las filas o las columnas en una representación gráfica de una matriz de dimensión $m\times n$ , se tiene el siguiente aspecto:

\boldsymbol{\color{red}{a_{12}}}

es el nombre del elemento que está en la 1ra fila y 2da columna.

\boldsymbol{\color{purple}{a_{21}}}

es el nombre del elemento que está en la 2da fila y 1ra columna.

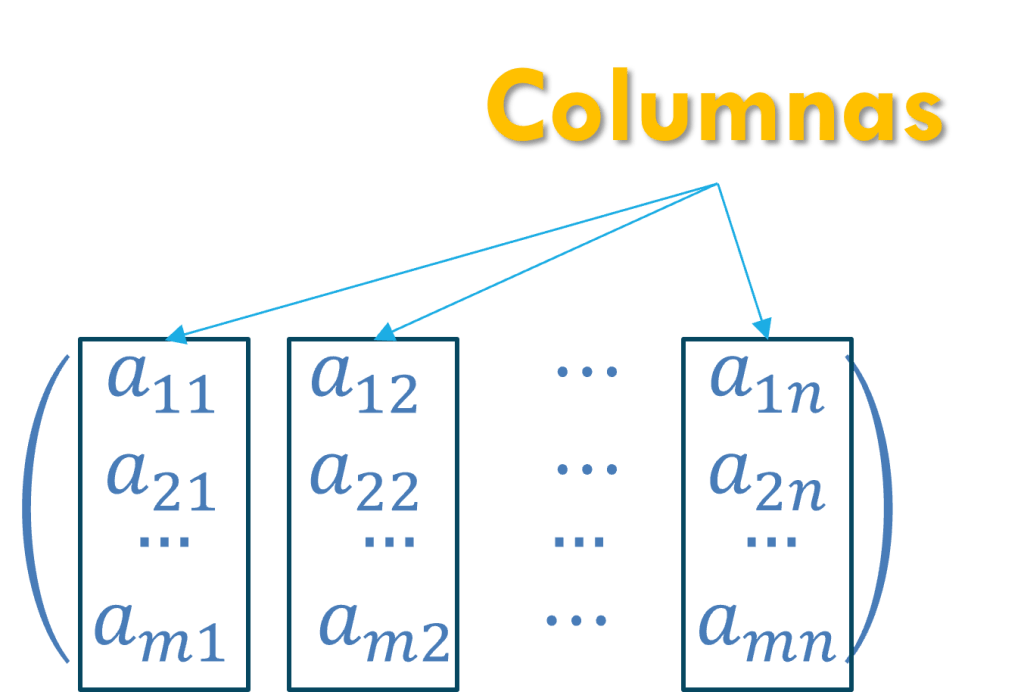
Tipos básicos, Igualdad y transposición de matrices.

Algunos tipos básicos de matrices.

Matriz Rectangular: Matriz de dimensión $\small\boldsymbol{m\times n, \quad n,m\in \mathbb{N}}, \quad$ $\small\boldsymbol{m\neq n}$ . Ejemplo:

A=\left(\begin{array}{lcc} -1 & 0 & \boldsymbol{{\color{red}-5}}\\ 4 & \boldsymbol{{\color{purple}3}} & -2 \end{array}\right) \in M_{2\times 3}

es una matriz rectangular de dimensión $2\times 3.$ Siendo, por ejemplo, $\small \boldsymbol{\color{red}{a_{13}=-5}},$ $\small \boldsymbol{\color{purple}{a_{22}=3}},$

Por el contrario, decimos de una matriz de dimensión $\small\boldsymbol{n\times n, \, n\in \mathbb{N}},$ que es una Matriz Cuadrada. En este caso también usamos la expresión que la matriz es de orden $\boldsymbol{n}$ . El conjunto de todas las matrices de orden $\boldsymbol{n}$ lo denotamos simplemente por $\boldsymbol{M_n}.$ Ejemplo

A=\left(\begin{array}{lccc} 2 & -1 & {\color{red}\boldsymbol{0}} & 3\\ 1 & 2 & 4 & 5\\ 2 & 0 & 1 & -1\\ -1 & {\color{purple}\boldsymbol{7}} & 1 & 0 \end{array}\right) \in M_4

A

es una matriz cuadrada de orden 4 o de dimensión

4\times 4

\small \boldsymbol{\color{red}{a_{13}=0}},

\small \boldsymbol{\color{purple}{a_{42}=7}}

Matriz Fila: matriz que consta de una sola fila, es decir de dimensión $1\times n$ .

A=\left(\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n}\end{array}\right)

Matriz Columna : matriz que consta de una sola columna, es decir de dimensión $m\times 1$ .

Ejemplo:

a) Escribe la matriz $A$ de dimensión $3\times 2$ cuyos elementos son de la forma

a_{ij}=(-1)^{i+j}(i^2-5j)

Solución

A=\left(\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22}\\ a_{31} & a_{32} \end{array}\right)=\left(\begin{array}{cc} -4 & 9\\ 1 & -6\\ 4 & 1 \end{array}\right) \\ \, \\ a_{11}=(-1)^{1+1}(1^2-5·1)=-4 \\ \, \\ a_{23}=(-1)^{2+3}(3^2-5·2)=1

b) Escribe la matriz columna $B$ de dimensión $4\times 1$ cuyos elementos son de la forma

b_{ij}=2j-i

Solución:

B=\left(\begin{array}{c} b_{11}\\ b_{21}\\ b_{31}\\ b_{41} \end{array}\right)=\left(\begin{array}{c} 1\\ 0\\ -1\\ -2 \end{array}\right) \\ \, \\ b_{11}=2·1-1=1 \\ \, \\ b_{14}=2·1-4=-2

Igualdad de Matrices.

Dos matrices son iguales si:

Tienen la misma dimensión
Los elementos “dispuestos” en la misma fila y misma columna son respectivamente iguales.

A=B \Leftrightarrow a_{ij}=b_{ij}, \forall i,j

Ejercicio 1: Encontrar los valores de $t, x, y, z$ para que las siguientes matrices sean iguales:

A=\left(\begin{array}{cc} 3 & 2\\ t & 0 \end{array}\right), \quad B=\left(\begin{array}{cc} x & y\\ -3 & z \end{array}\right)

Solución:

A=B \Rightarrow \left\{ \begin{array}{l} 3=x\\ 2=y\\ t=-3\\ 0=z \end{array}\right.

Ejercicio 2: Encontrar los valores de $t, x, y, z$ para que las siguientes matrices sean iguales:

A=\left(\begin{array}{ccc} t+1 & 2t+1 & 2\\ y-2 & 3-t & 6 \end{array}\right), \quad \\ \, \\B=\left(\begin{array}{cc} 3 & x+1 & z-1\\ 2y & 1 & 2x \end{array}\right)

Solución:

A=B \Rightarrow \left\{ \begin{array}{l} t+1=3 \Rightarrow t= 2\\ 2t+1 = x+1 \Rightarrow x= 4 \\ 2=z-1 \Rightarrow z= 3 \\ y-2= 2y \Rightarrow y= -2 \\ \color{green}{3-t=1 \Rightarrow t= 2} \\ \color{red}{6=2x \Rightarrow x= 3} \end{array}\right.

No existen valores para estas variables para que ambas matrices sean iguales ( $x$ no puede tomar simultáneamente el valor 3 y 4.